2021. 2. 5. 17:50ㆍ필요/코딩테스트(백준)

풀이
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> a[1001];
bool check[1001];
void dfs(int node) {
check[node]=true;
for (int i=0; i<a[node].size(); i++) {
int next = a[node][i];
if (!check[next]) {
dfs(next);
}
}
}
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i=1; i<=n; i++) { // 사용한 공간 초기화
a[i].clear();
check[i]=false;
}
for (int i=1; i<=n; i++) { // 방향 그래프 입력
int v;
cin >> v;
a[i].push_back(v);
}
int cnt=0;
for (int i=1; i<=n; i++) { // 각 탐색마다 count + 1
if (!check[i]) {
dfs(i);
cnt++;
}
}
cout << cnt << '\n';
}
return 0;
}개념
방향 그래프

그래프는 무방향 그래프와 방향 그래프로 나뉜다.
방향 그래프는 한쪽으로만 이동할 수 있다. A-> B는 가능하지만, B->A는 불가능한 것이다.
사이클

풀이
입력되는 값이 이전과 상당히 다르다.
예시를 보자면, 테스트 케이스를 거치고
8
3 2 7 8 1 4 5 6
이렇게 입력된다.
문제 설명을 보면 이는 node가 0~8이고
1 2 3 4 5 6 7 8
↓↓↓↓↓↓↓↓
3 2 7 8 1 4 5 6
이렇게 간선이 있다고 생각하면 된다.
방향 그래프는 일방통행이므로, a[node]에 값을 push하는 형태로 입력을 받는다. (양쪽으로 push X)
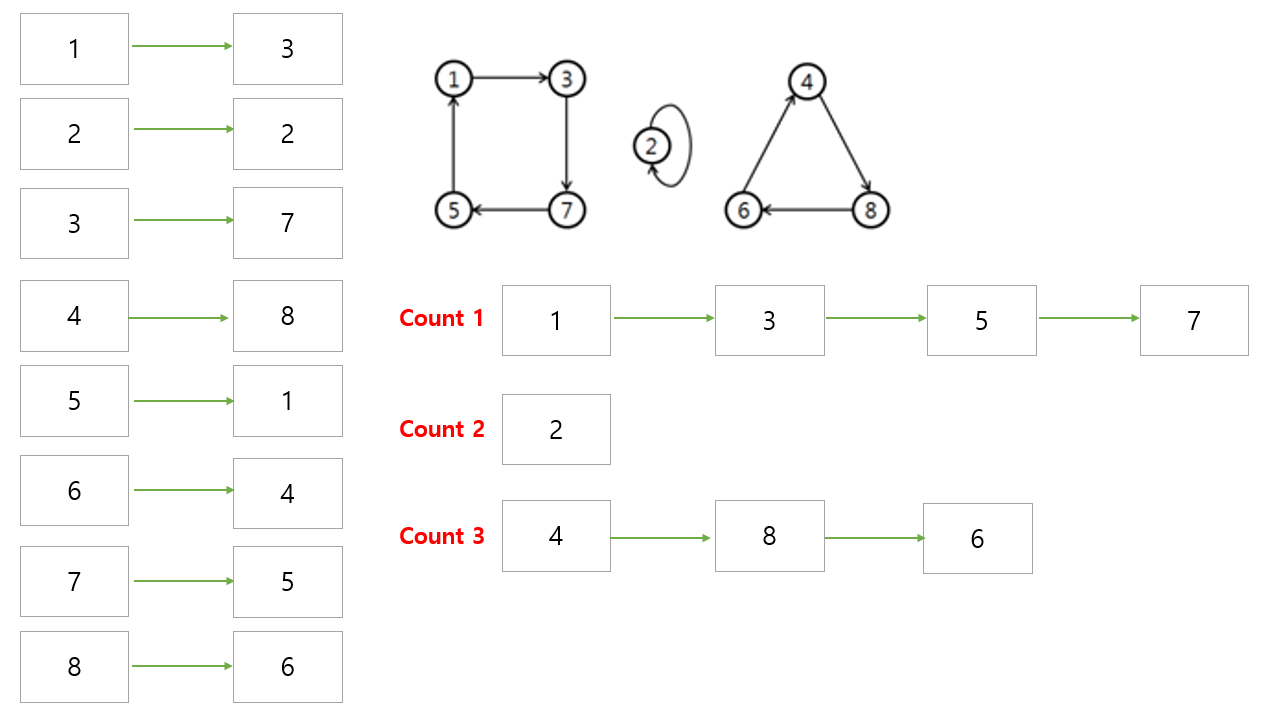
탐색은 연결된 모든 노드를 방문한다.
그렇다면 한번의 탐색은 그 노드와 연결된 사이클을 돈 것과 같다.
따라서 사이클의 개수는, main 함수에서 시작한 탐색의 개수와 같다.
이러한 논리로, for문 안에서 탐색이 반복 될 때마다 cnt + 1 한다.
+a
다른풀이①(압축)
void dfs(int node) {
check[node]=true;
int next = a[node][0];
if (!check[next]) {
dfs(next);
}
}
주어지는 input의 형태가 매우 간단하므로, 하나의 노드에 한 개의 노드만 연결된다.
따라서 dfs 함수를 아예 변형하여 위처럼 간단하게 표현 할 수 있다.
이는 이번 문제에서 리스트를 따로 정렬하지 않는 이유이기도 하다.
다른풀이②(from 백준github)
#include <iostream>
using namespace std;
int a[1001];
bool c[1001];
void dfs(int x) {
if (c[x]) return;
c[x] = true;
dfs(a[x]);
}
int main() {
int t;
cin >> t;
while (t--) {
int n;
cin >> n;
for (int i=1; i<=n; i++) {
cin >> a[i];
c[i] = false;
}
int ans = 0;
for (int i=1; i<=n; i++) {
if (c[i] == false) {
dfs(i);
ans += 1;
}
}
cout << ans << '\n';
}
return 0;
}원리는 동일하다. 다만, 굳이 이차원 배열을 만들지 않고, 일차원 배열로 만들어서 더욱 압축을 했다.
살짝 걸리는 부분이 있다.
문제에서는 분명 입력으로 주어진 순열에 존재하는 순열 사이클의 개수를 출력하라고 했다.
예제에서는 같았지만, 모든 경우에서 사이클의 개수가 탐색의 개수와 같은지는 의문이다.
반례로, 1->2->1 의 사이클이 아닌 1->2 인 경우에도 탐색이 끝나서 cnt가 +1 되기 때문이다.
이 부분은 좀 더 고민해 봐야겠다...
'필요 > 코딩테스트(백준)' 카테고리의 다른 글
| [백준/C++]#9466 - 텀 프로젝트 (0) | 2021.02.09 |
|---|---|
| [백준/C++]#2331 - 반복수열 (0) | 2021.02.07 |
| [백준/C++]#1707 - 이분 그래프 (0) | 2021.02.04 |
| [백준/C++]#11724 - 연결 요소의 개수 (0) | 2021.02.04 |
| [백준/C++]#1260 - DFS와 BFS (0) | 2021.02.02 |